In 2017, O. Kochukhov (A&A 597, A58) published a paper titled "Doppler imaging of chemical
spots on magnetic Ap/Bp stars: Numerical tests and assessment of systematic errors".

The assumptions underlying the tests were the following (quoting O.K. verbatim):

  "Two different Fe surface abundance distributions were considered in the numerical experiments.
   The first comprised four circular overabundance spots, with log (N_Fe /N_tot) = −2.5 in the
   spot centres and log (N_Fe /N_tot) = −4.0 in the background. The spots were placed at the
   latitudes of −30, 0, 30, and 60◦ and spaced equidistantly in longitude. We adopted the inner
   spot radius of r_in = 15◦ and the outer radius of r_out = 30◦. The element abundance was
   linearly interpolated between r_in and r_out, resulting in smooth spot edges.

   This multiple spot configuration is more complex than the three-spot abundance map previously
   considered in the numerical tests of Invers10 (Kochukhov & Piskunov 2002)."

The conclusions are formulated in (again O.K. verbatim):

  "Our DI code achieves an average accuracy of 0.06–0.09 dex and maximum errors of 0.12 dex for
   the chemical map reconstruction which includes magnetic field effects in spectrum synthesis
   and is based on about half a dozen of individual spectral lines [for a complex element
   distribution comprised of multiple circular element overabundance spots}

   A reduction of the line list to one or two spectral features, including a blended one, leads
   to only a marginal increase of the average inversion errors to about 0.1 dex and maximum errors
   to ∼0.15 dex. Therefore, apart from counteracting random observational noise, abundance DI
   inversions do not gain significantly from modelling a large number of spectral lines.

   Ignoring a moderately strong, 2.5 kG dipolar magnetic field in abundance DI introduces a mean
   offset of about 0.3 dex in the recovered chemical maps. The average relative reconstruction
   errors increase to ∼0.2 dex while the maximum relative errors reach ∼0.3 dex. These errors
   correspond to distortions of real surface abundance inhomogeneities. The spurious component
   of abundance maps (i.e. Zeeman broadening and intensification misinterpreted as abundance
   variations) does not exceed ∼0.15 dex on average."

Of course, up to 2017 astrophysics has not been aware of a single published abundance map of a
magnetic CP star which would show 3 or 4 circular spots, well ordered both in latitude and in
longitude, and with perfectly smooth spot edges. Not surprisingly, 5 years later, these objects
yet have to be detected. This certainly represents a major problem: it can well be argued that
to flatly extrapolate O.K.'s claims and findings to actual stars (such as HR3831 and many others)
without expressing a multitude of caveats would not constitute a strictly canonical scientific
approach. Is there a solution to this dilemma?

Fortunately, a wealth of data are provided by O.K. and collaborators which allow scientists
from outside the INVERS-based group of ZDM aficionados to carry out their own investigations
and to come to their own conclusions, independently of rival ZDM codes (see Stift 1996 to 2022),
or of physical assumptions and data sets different from those used by the Uppsala centred group.

Simply look at the literature and you will find that a number of magnetic CP stars have been
analysed several times. Some of these analyses and reanalyses are based on a single set of
observations -- such as 53 Cam which inexplicably has never been observed again after the
2004 paper -- whereas others rely on different data sets obtained over the years -- such as
HD24712.

HD3980 has elicited particular attention on account of a wealth of physical inconsistencies
underlying the analysis by Nesvacil et al. (2012). There can be little doubt that the maps
published are entirely spurious as detailed in

       https://www.ada2012.eu/open/index.html

but as it turns out, they are still highly useful for error analysis when confronted with those
by Obbrugger et al. (2008). Just compare the Cr maps shown in their Fig.2 with those in Fig.6
of Nesvacil et al. (2012). One immediately notes the huge difference in contrast between the
two: -7.0 to -1.5 in 2008, -5.3 to -2.3 in 2012. In both cases, the magnetic field has been
neglected, varying assumptions as to the geometry therefore do not explain the difference. The
adopted inclination is almost identical (65 vs. 60 deg), 20 spectra with a S/N ratio of about
300 are in common, 11 spectra with S/N ~ 150-200 have been added in 2012. 2 Cr lines have been
used in 2012, probably 3 Cr lines in 2008.

Following Kochukhov (2017) the maximum difference between the 2 sets of maps should not exceed
0.15 dex. Difference plots in the sense 2012-2008 -- for phases 0.0, 0.2, 0.4, 0.6, 0.8, from
left to right -- however prove to be completely at variance with these expectations/predictions



We observe staggeringly large differences, going from at least -1.5 dex to more than 2.0 dex,
i.e. up to 15 times larger than the maximum given by O.K. !! Please note that my plots are
omitting the outermost parts of the visible hemispheres, the published plots being of poor
quality, full of artefacts near the borders.

These findings call forth a number of questions:

• Why is there no discussion in Nesvacil et al. (2012) of the huge discrepancies between
  the 2012 and the 2008 chromium maps ? Not a single sentence, not even a single word is
  spent on the 2008 inversions.
• How can one explain the fact that the respective fits to the observed Cr lines are of
  the same (moderate) quality -- with deviations of up to 2% -- for both papers, leading
  however to completely different maps ?
• Why has O.K. in 2017 not chosen actual inversions for his error analysis instead of
  highly artificial spot geometries not found in any of the numerous inversions carried
  out with the help of his INVERS codes ?
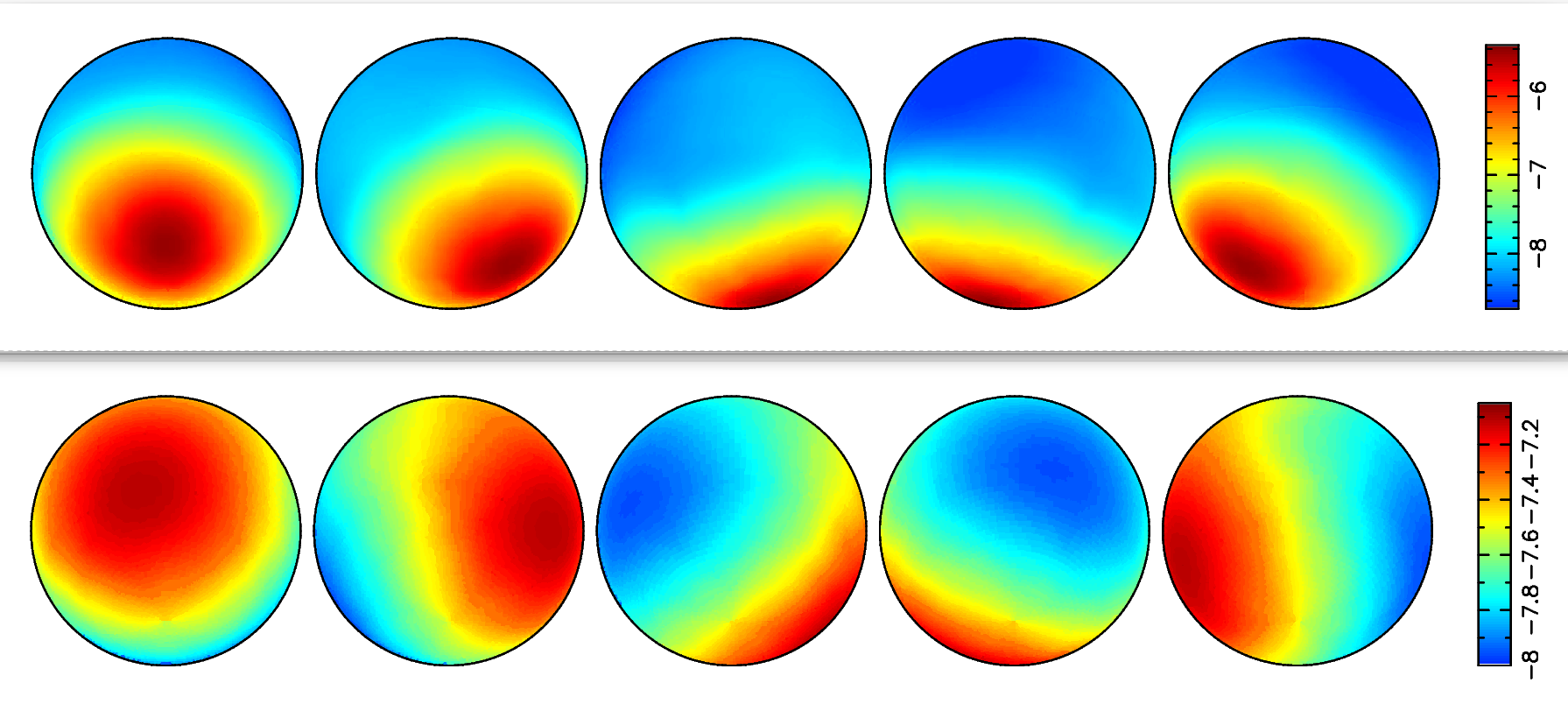
• Could O.K. not better have illuminated us with a discussion of HD24712 where abundance
  contrasts have more than doubled between Lüftinger et al. 2010 (bottom) and Rusomarov
  et al. 2015 (top), and where spots change position? Wouldn't everyone like to have it
  explained how "The new maps confirm the previous findings, and also show some details
  not present in the previous study" ?

    

  Back to the Ada in Astrophysics Homepage