The Paschen-Back effect in stellar Stokes spectra

    modelled thanks to Ada

A concise explanation of the basic physical facts by Prof. Egidio Landi Degl'Innocenti

Let us consider a term of an atom, characterised by the quantum numbers L and S. The term is composed of 2S+1 (or 2L+1 if L < S) J-levels whose energy separation is due to the spin-orbit interaction. When a weak magnetic filed is present, each J-level splits into 2J+1 magnetic sublevels that can be identified by the further quantum number M. In as far as the magnetic splitting is much lower than the fine-structure separation between different J-levels, such splitting turns out to be proportional to the magnetic field, and the atom is said to be in the Zeeman effect regime. However, when the magnetic field starts to be comparable, or even larger than the fine-structure separation between J-levels, the linearity property is lost and the atom enters the regime of the (incomplete) Paschen-Back effect. Here the situation is more complicated because the quantum number J is no longer a good quantum number and the atomic levels can thus be characterised only by the magnetic quantum number M, not by J.

Multi-processor and/or multi-core architectures in conjunction with modifications to the object-oriented and parallel COSSAM code (Stift 2000)  have made it possible - since early 2006 - to model stellar Stokes spectra in the incomplete Paschen-Back regime. The new CossamPaschen code calculates (for realistic stellar atmospheres) detailed Stokes spectra of a multiplet in the incomplete Paschen-Back regime, with full blending from the remaining lines included, assuming classical anomalous Zeeman patterns for the latter. Provision is made both for the solar case and the stellar case (adopting an Oblique Rotator Model with a decentred dipole magnetic geometry).

During the CP#AP workshop in Vienna in September 2007 I showed high resolution Stokes profiles of the FeII lines at 6147 and 6149 in strongly magnetic Ap stars, synthethised for various Oblique Rotator models,  and illustrating the asymmetries and line-shifts introduced by the incomplete Paschen-Back effect. It was the first time ever that stellar Stokes profiles - correctly integrated over the visibile hemisphere, with an accurate formal solution to the polarised equation of radiative transfer in a realistic stellar atmosphere - of any spectral line subject to the PB effect have been presented.


Here is a nice illustration of the Paschen-Back effect




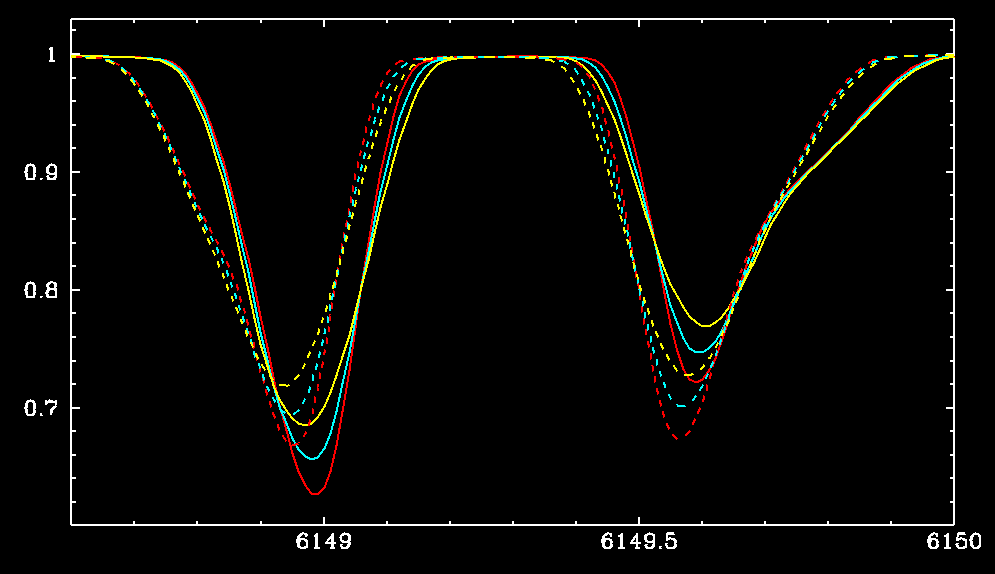
Oblique Rotator Models with H_s = 14500 Gauss

red:        3 km/s              full lines :          Paschen-Back
cyan:     4 km/s  
yellow:  5 km/s              dashed lines :  Zeeman

Note the conspicuous shifts between Zeeman and Paschen-Back profiles

  Back to the Ada in Astrophysics Homepage